O ensino da fração no início do Ensino Fundamental é tão importante quanto qualquer processo de ensino aprendizagem de matemática. Sobre esse estudo leu-se que elas diferenciam entre si de acordo com a sua representação e consequentemente sua escrita.

Considerando tal importância assinale a alternativa que apresenta a escrita correta das frações representadas nos desenhos abaixo.

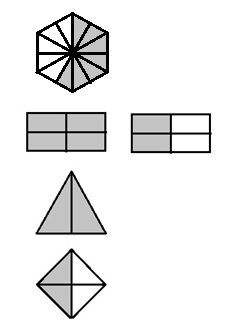
7/12,   1  2/4   ou   6/4,    2/2,    4/2

7/12,    1  4/2   ou   4/6,    2/2,     4/2

7/12,    1  2/4    ou   6/4,    2/2,    2/4

12/7,   1  2 /4   ou   6/4,    2/2,     4/2

12/7,   1  4/2   ou   6/4,   2/2,     4/2

– Um número é múltiplo de outro quando o primeiro é resultado da multiplicação entre o segundo e algum número natural. Nesse mesmo caso, também é possível dizer que o segundo é divisor do primeiro.

6 : 2 = 3    logo,    2 x 3  = 6

Fazendo uma analogia sobre a associação entre divisores e múltiplos, temos que: se 6 é divisível por 2, então, 6 é multiplo de 2.

Sobre multiplos e divisores temos as afirmativas abaixo. Leia-as analise e classifique-as em verdadeiro (V) ou falso (F). 

 

• 732 é divisível por 4 porque  o número 32 é também é divisível por 4.       
• 0, 3, 6, 9, 12, 15 e 18   são múltiplos de 3  menores que 20.
• 1, 2, 3, 4, 6, e 12  são multiplos de 12.
• 342  é divisível por 1, 2, 3, 6 e por 9
• 42, 49, 56, 63  são múltiplos de 7 compreendidos entre 40 e 70. 

É correto apenas o que se afirma em:

V, V, F, V, F

V, V, V, V, V

F, V, F, V, V

V, V, F, V, V

V, F, F, V, V

Na geometria, os conceitos de área e perímetro são utilizados para determinar as medidas de alguma figura. A área é a medida de uma superfície e o perímetro é a medida do comprimento de um contorno.

 

Um triangulo retângulo base 10 cm e os lados medindo 8 cm e 18 cm, tem como área ___________ e perímetro _________________.

 

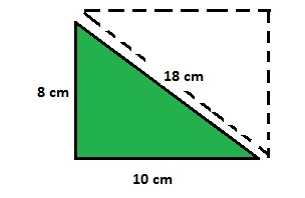
 É correto o que se afirma em:

área 40 cm² , perímetro 36 cm.

área 36 cm² , perímetro 40 cm.

área 18 cm² , perímetro 80 cm.

área 40 cm, perímetro 36 cm².

área 36 cm, perímetro 40 cm².

No grupo dos sólidos geométricos temos aqueles que deslizam e os que rolam. Os que deslizam apresentam quinas ou cantos, como é o caso das caixas que são os poliedros, e os que rolam são os corpos redondos, os quais apresentam sua superfície arredondada (latas, bola, funil e cilindro).

Os poliedros recebem esta nomenclatura por possuírem várias faces. As faces dos poliedros são figuras planas (quadrado, retângulo, hexágono dentre outros). As caixas são exemplos de poliedro. Os triângulos são figuras planas, porém, não fazem parte do grupo dos poliedros, eles fazem parte do grupo das pirâmides. 

 Leia as alternativas abaixo e assinale a única errada.

Um retângulo com 5 cm de comprimento por 3 de altura, tem uma área de 8 cm².

O perímetro de um triângulo equilátero, cujos lados medem 4 cm é 12 cm. 

O cubo bem como o paralelepípedo tem 8 vértices, 12 arestas e 6 faces.

O poliedro com 20 faces é denominado como icosaedro.

Um triângulo com 8 cm de base e 3 cm de altura, tem uma área de 12 cm². 

No contexto da Geometria o estudo dos triângulos é um dos mais importantes, para não dizer o mais importante de todos. Os triângulos são polígonos de três lados, três ângulos e três vértices, e é uma figura plana. Quando falamos que é o mais importante é no sentido, de possuir várias aplicações no nosso cotidiano. São utilizados nas construções de telhados, porteiras, instrumento musical, nas colunas de sustentação de pontes, dentre outros.

Eles podem ser classificados de duas formas: em relação aos lados e aos ângulos. Com base nesse estudo leia as afirmativas abaixo e classifique em verdadeiras ou falsas. Em seguida, assinale a sequencia correta.

A - Triangulo equilátero -possui todos os lados iguais.

B - Triângulo escaleno - possui todos os lados diferentes.

C - Triângulo isósceles -  possui dois lados congruentes, ou seja, dois lados iguais.

D - Triângulo acutângulo – possui todos os ângulos menores que 90°

E - Triângulo retângulo – possui um ângulo reto, ou, de 90º

F - Triângulo obtusângulo – possui um ângulo obtuso, ou, maior que 90º.

São verdadeiras as afirmativas A, D, E e F.

São verdadeiras as afirmativas  B, D e E.

Todas alternativas são verdadeiras.

São verdadeiras as afirmativas A, B, D e E.

São verdadeiras as afirmativas A, B, C, e F.

Mudando o método de ensino.

Uma das principais razões de a Matemática fazer parte do currículo do 1º Grau é o fato de queremos que os alunos saibam lidar com problemas cujas soluções envolvam conceitos matemáticos e, de alguma maneira, exijam o modo de pensar matemático.

Ensinar a resolver problemas é uma tarefa muito mais complexa do que ensinar algoritmos e equações. A postura do professor ao ensinar algoritmos é, a de um ordenador dando instruções, passo a passo, de como fazer. Na resolução de problemas, ao contrário, o professor deve funcionar como incentivador e moderador das idéias geradas pelos próprios alunos. Neste caso, as crianças participam ativamente “fazendo matemática”, e não ficam passivamente “observando” a Matemática “ser feita” pelo professor. É uma tarefa radical e importante mudança de método tradicional que consiste em mostrar e repetir, com base a expressão é assim que e faz. No chamado método heurístico, o professor encoraja o aluno a pensar por si mesmo, a levantar suas próprias hipóteses e a testá-las, a discutir com sues colegas como e por que aquela maneira de fazer funciona. (DANTE, 1989, p.52)

 

Assinale a única alternativa errada.

É importante que o problema possa gerar muitos processos de pensamento, levantar muitas hipóteses e propiciar várias estratégias de solução.

O professor deve saber diferençar exercício de problemas. Exercício serve para exercitar, para praticar determinado algoritmo ou procedimento. Situação-problema é a descrição de uma situação em que se procura algo desconhecido e não tem previamente nenhum algoritmo que garanta a sua solução.

Problemas com dados artificiais desmotivam o aluno. Os dados devem ser reais, quer nas informações nele contidas, quer nos valores numéricos apresentados.

A resolução de problemas deve se construir de experiências repetitivas, por meio da aplicação dos mesmos problemas (com outros números) resolvidos pelas mesmas estratégias.

As situações-problemas devem ser desafiadoras, motivadoras, que aumentem a sua curiosidade em pensar neles e querer resolvê-los.

“O ensino de Matemática costuma provocar duas sensações contraditórias, tanto por parte de quem ensina, como por parte de quem aprende: de um lado, a constatação de que se trata de uma área de conhecimento importante; de outro, a insatisfação diante dos resultados negativos obtidos com muita frequência em relação à sua aprendizagem”. (PCN Matemática, p.15. disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf ). 

Os PCNs de Matemática descrevem que a educação matemática é importante para a construção da cidadania. E que deve estar ao alcance de todos e a democratização do seu ensino deve ser meta prioritária  do trabalho docente. 

“A atividade matemática escolar não é olhar para coisas prontas e definitivas”, mas a construção e a apropriação de um conhecimento pelo aluno, que se servirá dele para compreender e transformar sua realidade’ “.”. (PCN de Matemática, p.19. disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf ).

 

Sobre o ensino da matemática temos que:

1.  A aprendizagem em Matemática está ligada à compreensão, isto é, à apreensão do significado; apreender o significado de um objeto ou acontecimento pressupõe vê-lo em suas relações com outros objetos e acontecimentos.
2. A seleção e organização de conteúdos não deve ter como critério único a lógica interna da Matemática. Deve-se levar em conta sua relevância social e a contribuição para o desenvolvimento intelectual do aluno. Trata-se de um processo permanente de construção. 
3. O conhecimento matemático deve ser apresentado aos alunos como historicamente construído e em permanente evolução. O contexto histórico possibilita ver a Matemática em sua prática filosófica, científica e social e contribui para a compreensão do lugar que ela tem no mundo. 
4. Recursos didáticos como jogos, livros, vídeos, calculadoras, computadores e outros materiais têm um papel importante no processo de ensino e aprendizagem. Contudo, eles precisam estar integrados a situações que levem ao exercício da análise e da reflexão, em última instância, a base da atividade matemática. 
5. O tratamento dos conteúdos em compartimentos estanques deve ser considerado, visto que, só assim o aluno compreenderá o significado da Matemática. 

  Estão corretas as afirmativas:

1, 2, 3 e 4 apenas.

1, 2 e 3 apenas.

1, 3 e 4 apenas.

1, 2 e 5 apenas.

1, 2, 3, 4 e 5.

Como a escrita dos números nos antigos sistemas de numeração era muito complexa e dificultava os cálculos, o homem criou vários instrumentos que auxiliavam a calcular e usava a escrita principalmente para registrar o resultado de contas. Uma das mais antigas máquinas de calcular, e que vem sendo usada há mais de mil anos, é o Ábaco.

“O ábaco é um antigo instrumento de cálculo, formado por uma moldura com varetas ou arames paralelos, dispostos no sentido vertical, correspondentes cada um a uma posição digital (unidades, dezenas,...) e nos quais estão os elementos de contagem (fichas, bolas, contas,...) que podem fazer-se deslizar livremente. Teve origem provavelmente na mesopotâmia, há mais de 5.500 anos. O ábaco pode ser considerado como uma extensão do ato natural de se contar nos dedos. Emprega um processo de cálculo com sistema decimal, atribuindo a cada haste um múltiplo de dez. Ele é utilizado ainda hoje para ensinar às crianças as operações de somar e subtrair". Disponível em: https://pt.wikipedia.org/wiki/%C3%81baco. Acesso em: 07/02/2017.

Considerando a aplicabilidade do Ábaco na resolução de operações pelas crianças avalie as afirmações abaixo sobre a utilização correta desse material.

I-  A contagem no Ábaco inicia-se da direita para a esquerda, na ordem das unidades.

II-  A contagem no Ábaco inicia-se da esquerda para a direita, na ordem das unidades.

III-  Ao utilizar o Ábaco é importante que os alunos percebam que o zero representa a casa vazia, ou seja, aquela que não tem marcação de continhas.

 IV-  Ao representar determinada quantidade no Ábaco a notação decimal estará de acordo com a posição das varetas.

V- No sistema de numeração decimal, nunca podem ficar dez peças na mesma posição, ou seja, na mesma vareta. Elas são imediatamente substituídas por outra peça e passadas para o vareta  seguinte de valor maior.

É correto apenas o que se afirma em:

II, III, IV, V

II, IV, V

I, III, IV, V

I, IV, V

III, IV

Uma figura geométrica é plana, quando todos os seus pontos estiverem em um mesmo plano, ou seja, a figura plana é apenas representada por desenhos, não conseguimos pegá-la. Já os sólidos geométricos possuem dimensão, ou seja, possuem volume. 

 

Acerca desta afirmação, classifique as afirmativas abaixo em Verdadeiras ou Falsas. 

• Um quadrado é uma figura geométrica plana.                                                  
• Um cubo é um sólido geométrico formado por 6 quadrados.                       
• O cone a esfera e o cilindro são sólidos geométricos, do grupo dos corpos redondos.   
• As pirâmides são sólidos geométricos, formados de triângulos, algumas podem ter a base quadrangular. Essa característica é fundamental para colocá-la no grupo dos prismas.  
• Um cubo possui 12 vértices e 8 arestas.    

Assinale a sequência CORRETA:

 

V, V, F, F, V.

V, V, V, V, V.

V, F, F, V, V.

V, F, V, V, F.

V, V, V, F, F.

O termo fração está relacionado a idéia de dividir um todo em partes iguais. Sobre as frações é incorreto afirmar que:

Em uma classe com 30 alunos, faltaram 15 alunos. A fração que representa esta situação é 15/30 ou 1/2.

As frações podem ser classificadas como própria (numerador maior que denominador), imprópria (numerador menor que o denominador), mista ( número inteiro e parte fracionária), equivalente ( frações que escritas de forma diferentes, mas, representam a mesma quantidade, aparente (numerador e denominadores iguais).

Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte que sobrou do chocolate é 1/6.

Ana comeu 2/6 da barra de chocolate. Sua irmã comeu 3/6. A fração que representa a parte comida do chocolate é 5/6.

 As frações 3/6, 6/12, e 1/2 são equivalentes.